JVER v27n2 - Using Structural Equation Modeling to Improve Research in Career and Technical Education
Using Structural Equation Modeling to Improve Research in Career and Technical Education
Heeja Kim Touro University International Jay W. Rojewski University of Georgia Abstract
This paper describes structural equation modeling (SEM) and possibilities for using SEM to address problems specific to workforce education and career development. A sample of adolescents identified as work-bound (i.e., transition directly from secondary school to work) from the National Education Longitudinal Study 1988-1996 database ( NELS: 88-94, 1996 ) 1 was selected for illustrative purposes. The authors urge greater use of sophisticated analytic techniques like SEM in career and technical research to more adequately consider the complexity of work-based issues and problems.Measurement ModelThe use of structural equation modeling (SEM) to examine complex questions in education and the social sciences has seen substantial growth in popularity over the past decade. The increase in use can be attributed to a number of things including a greater flexibility in representing relationships among theoretical constructs, ability to posit latent constructs presumed to be underlying causes of observed manifest variables, and ease in evaluating the general compatibility or "goodness of fit" of a proposed model for the data being examined and the strength of relationships among constructs ( Quintana & Maxwell, 1999 ).
Covariance structural modeling, another term for SEM, integrates the best of several analyses including multiple regression (directional relationships between a set of predictor variables and a dependent [or criterion] variable), path analysis (tests for theoretical relationships among independent and dependent variables, and the direct and indirect effects of independent variables on dependent ones), and factor analysis (determining which variables have common variance-covariance characteristics with a latent variable of construct ( Breckler, 1990 ; Kunnan, 1998) . SEM procedures emphasize covariances rather than cases, and attempt to minimize the difference between sample covariances and covariances predicted by the model ( Bollen, 1989 ). 2
Although the family of statistical analyses based on SEM have been applied to numerous empirical investigations in education and the social sciences, scholars in career and technical education have been somewhat slow to adopt the techniques for their research. Rojewski (1997b) reported that in the 10-year period, 1987-1996, only two articles (1.9%) published in the Journal of Vocational Education Research used SEM. The low level of interest in SEM is probably due to a host of factors, the chief ones likely being a lack of pedagogic instruction on SEM and related topics, few quality examples of SEM application to issues of concern to the field, little discussion of the merits and limitation of SEM among scholars in career and technical education ( Kunnan, 1998 ), and the limited use of theory guiding career and technical education research ( Rojewski, 1999 ).
Therefore, this paper introduces the general uses of SEM and reviews its potential application in career and technical education research. We illustrate the principles of SEM using an issue of some importance to career and technical educators: the development and implementation of career aspirations espoused by work-bound youth. Occupational aspiration and its role in career choice have stimulated a considerable amount of empirical research focusing on wide-ranging topics such as the role of aspirations in career compromise and comprehension ( Lapan & Jingeleski, 1992 ; Leung, 1993 ; Leung & Plake, 1990 ), the effectiveness of early aspirations in predicting career choice and attainment ( Holland, Gottfredson, & Baker, 1990, ), the influence of aspirations on pursuit of educational and occupational opportunities ( Lent, Brown, & Hackett, 1996 ), and the impact that factors like gender have on aspirations ( Davey & Stoppard, 1993 ). While substantial progress has been made in establishing the nature and determinants of occupational aspirations, much remains to be examined about the possible antecedents of aspirations and their role in career behavior ( Osipow & Fitzgerald, 1996 ), especially for adolescents who will transition directly from secondary school to work.
What is Structural Equation Modeling?
Bollen (1989) offers the fundamental hypothesis for structural equation modeling:
Σ = Σ(Θ)Where Σ (sigma) is the population covariance matrix of observed variables, Θ (theta) is a vector of model parameters, and Σ(Θ) is the covariance matrix implied by the model. When the equality expression in the equation holds, the model is said to "fit" the data. However, it is highly unlikely that a perfect fit will exist between the observed data and the hypothesized model, and there will necessarily be a discrepancy, which is termed the residual, between the two. byrne (1998) therefore summarized the model-fitting process as:
Data = Model + ResidualData represents score measurements related to the observed variables as derived from persons comprising the sample. Model represents the hypothesized structure linking the observed variables to the latent variables, and in some models, linking particular latent variables to one another. Residual represents the discrepancy between the hypothesized model and the observed data.
Typically, a researcher postulates a statistical model based on his or her theoretical knowledge, on empirical research related to the study, or some combination of both ( Pedhazur, 1997 ). Once specified, the plausibility of the model is tested using a computer program, e.g., LISREL (Linear Structural Relations Analysis), based on sample data comprising all observed variables in the model.
In LISREL, a computer program that performs SEM 3 ( Joreskog & Sorbom, 1996 ), exogenous variables are designated as ξ (xi) and endogenous variables are designated as η (eta). Exogenous variables, which are used as predictor or independent variables, are considered to be the starting points of the model, and endogenous variables may serve as both predictors and criteria, being predicted by exogenous variables and predicting other endogenous variables. The model in SEM has two basic components: the measurement model, which defined hypothetical latent variables in terms of observed measured variables, and the structural model, which defines relations among the latent variables ( Breckler, 1990 ).
Structural ModelSEM is a powerful analytic procedure that allows examination of fairly complex theoretical models or patterns of relationships among latent variables. 4 This is accomplished through the simultaneous specification and analysis of measurement and structural equation models. A measurement model is concerned with relationships between one or more observed (measured) variables, such as scores from rating scales or questionnaire items, and a latent (unobserved or hypothetical) variable. Typically, confirmatory factor analysis is used to define underlying or latent constructs represented by observed (measured) variables. Construction of a measurement model follows the general logic of factor analysis where multiple measures of a theoretical domain are obtained and specific components of each measure related to the latent variable is extracted ( Bollen, 1989 ; Joreskog & Sorbom, 1989 ; Moore, 1995 ).
To develop a measurement model, the range of theoretical constructs included in the model and the way constructs will be measured must be considered ( Quintana & Maxwell, 1999 ). For our example, we are interested in the stability or volatility of aspirations espoused by work-bound youth from the 8th to 10th grades ( Rojewski, 1997a ). While illustrative, this example is relevant to those in career and technical education since developmental theory ( Super, 1990 , Super, Savickas, & Super, 1996 ) suggests that early adolescence is a time when individuals are increasingly aware and beginning to think about exploring various career-related opportunities. The more unstable adolescents' aspirations are, the less likely they are to make sound decisions regarding curriculum and other educationally-related issues.
Adolescents who are ambivalent or undecided about their occupational futures, as well as those with lower-prestige aspirations, may be less likely to enroll or persist in prerequisite academic courses in middle school, which may preclude their enrolling in more advanced courses in high school. This in turn, reduces the likelihood of pursuing postsecondary education and diminishes opportunities for attaining higher-prestige occupations. ( Rojewski, 1997a )
To construct our measurement model we chose two observed or measured variables-occupational aspirations and educational aspirations-to represent our unobserved dependent variables, postsecondary aspiration at Grade 8 and 10. Occupational aspiration was measured by participants' declaration of the occupation they expected or planned to have at 30 years of age from a listing of 17 separate occupations. These 17 occupations were organized into high, medium, and low prestige categorizes using socio-economic index codes that reflected perceived prestige levels and required education ( Stevens & Cho, 1985 ). Educational aspirations were determined by asking adolescents to denote the highest level of education they thought they would achieve. Educational aspiration was conceptualized as an interval-level construct ( Haller & Virkler, 1993 ) with a low score of 1 representing aspirations for high school and a high score of 6 representing aspirations for a PhD, MD, or equivalent. Figure 1 illustrates part of the measurement model. An identical model was also developed for examining postsecondary aspirations in Grade 10.
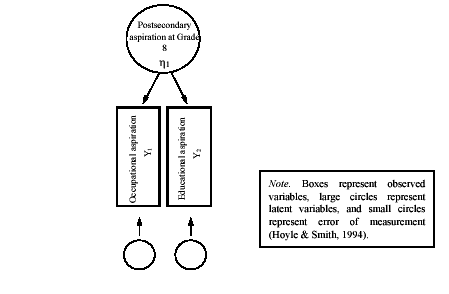
FIGURE 1. Example of a measurement model used in SEM.
The structural model is that part of structural equation modeling concerned with the relationships among the unobserved (latent) variables. Typically, the structural portion of the model simultaneously tests the effects of latent variables on each other ( Buczynski, 1994 ). A regression equation represents the simplest structural model where an observed independent variable influences an observed dependent variable ( Keith, 1993 ). While the general use of SEM involves both a measurement model and a structural model that tests latent (unobserved) variables ( Fassinger, 1987) , SEM can also be used without latent variables and is similar to analysis of variance or multiple regression where all possible paths are examined ( Bollen, 1989 ; Hoyle & Smith, 1994 ; Joreskog & Sorbom, 1989 ; Moore, 1995 ).
When designing a structural path model, several decisions must be made including (a) determining which latent (and observed) variables should be included in the model, and (b) specifying the paths of influence that should be examined. The first step is to specify a model which visually represents the hypothesized relationships of interest. Because of the potential complexity involved in specifying a structural model, researchers must rely on a strong theoretical basis, prior research, actual or logical time antecedent and precedents ( Rojewski, 1996 ). Typically, structural equation modeling will illustrate the relationships between observed variables and the latent variables they are hypothesized to represent (i.e., the measurement model), and the relationships between the latent variables (i.e., the structural model).
Figure 2 portrays the complete structural equation model we developed to examine the stability of postschool aspirations of work-bound adolescents. In terms of model notation, the symbol X denotes a pseudo-exogenous (ξ) variable, a variable that is not dependent on other variables within this model. The symbol Y denotes an endogenous variable which is dependent on one or more other variables in the model. Endogenous variables are the target of at least one one-headed arrow in any structural model.
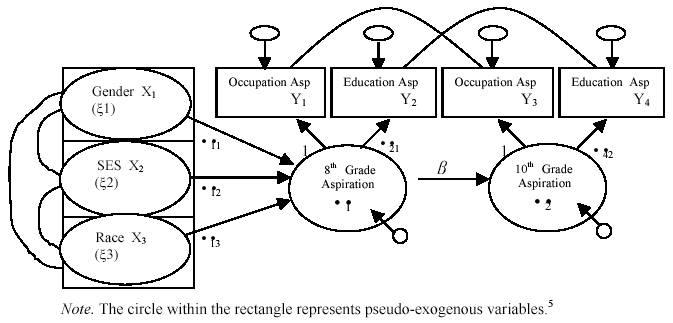
FIGURE 2. Model for testing relationships among occupational aspirations of work-bound youth from Grades 8 to 10.
Variable Specification
Information about gender, race/ethnicity, and socioeconomic status (SES) was collected from students' first follow-up questionnaires completed during Grade 10. Students were asked to indicate their racial/ethnic origins from predeveloped categories that were recoded for analytic purposes into White and nonWhite. This decision was based on a view that variables like race/ethnicity are stimulus variables that cause societal reaction such as bias or discrimination. We reasoned that regardless of specific group affiliation, individuals of minority status are more likely to share certain experiences and environmental barriers to educational and career attainment ( Osipow & Fitzgerald, 1996 ). Treating race as a dichotomous variable also facilitated the causal modeling analysis.
Occupational aspirations were assessed in grades 8 and 10 by asking adolescents to indicate the job or occupation they expected to have at age 30 from a listing of 17 distinct occupational categories used extensively by the U.S. government in census and survey work. Occupational aspirations were coded using the socioeconomic index (SEI) codes calculated by Stevens and Cho (1985) . Since the 4-digit SEI codes reflect income, social status expectations, and educational attributes of occupations, they allow differentiation between occupations along a socioeconomic hierarchy, providing a continuous rather than categorical variable ( Hotchkiss & Borow, 1996 ). Educational aspiration was coded on a 6-point Likert-type scale from high school to doctoral program.
Data Analysis
We used a latent variable modeling technique called multiple indicators, multiple causes (MIMIC), which is one of several structural equation models available on LISREL 8.14 software ( Joreskog & Sorbom, 1993 ). MIMIC models ( Joreskog & Goldberger, 1975 ) are a specific type of latent variable analysis that contains one or more latent variables that are simultaneously identified by both multiple endogenous item indicators (items that compose the measure under consideration) and by multiple exogenous causal variables (background variables such as demographics).
Figure 2 contains the MIMIC model of career aspirations employed in our analysis. Exogenous variables include gender, SES, and race. These are used like pseudo-exogenous latent variables in this MIMIC model. That is, X is a perfect measure of ξ and that only one latent variable, η1 is present. The η1 is directly affected by one or more X variables, and it is indicated by one or more Y variables. Latent endogenous variables η) are represented by occupational aspirations educational aspirations. The structural model relating exogenous (X) and endogenous (Y) variables consists of • • (gamma, structural coefficients relating X to Y variables) and • •(beta, structural coefficients relating Y to Y variables) matrices. We let the measurement error of the indicators between Grades 8 and 10 correlate since the same measures are repeated over time resulting in a tendency for measurement errors to correlate over time due to memory or other retest effects ( Joreskog & Sorbom, 1996 ).
A two-factor measurement model (8th and 10th grades), including the direct effects of exogenous variables-gender, SES, and race-on latent variables representing 8th and 10th grade aspirations, was estimated for work-bound adolescents. The model was estimated on the covariance matrix with maximum likelihood estimation and was identified by the MIMIC rule outlined by Bollen (1989) ; when the number of Ys (endogenous indicators) is two or greater and the number of Xs (exogenous variables) is one or more then a sufficient condition exists for identification. The equations for the MIMIC model are: η = • • η + Γx + ζ;y = Λ y η +ε; and x = ξ. In the equations, η is the vector of latent endogenous random variables; ξ is the latent exogenous random variables; • • is a coefficient showing the influence of the latent endogenous variables on each other; Γ is a coefficient for the effects of ξ on η; ζ is the disturbance vector that is assumed to have an expected value of zero and which is uncorrelated with ξ; y and x vectors are observed variables; Λ is a coefficient that shows the relation of y to η; ε is the error of measurement for y.
Two variables-occupational aspiration and educational aspiration at grades 8 and 10, respectively-were used as indicators of adolescents' postsecondary career aspiration. Background variables were respondents' gender, socioeconomic status, and race. Female students were slightly more likely to report higher aspirations than male students (• • = .139); nonwhite students were slightly more likely to report higher aspiration than white students (• • = -.156). However, socioeconomic status (SES) had considerable influence on reporting their transition status (• • = .424) supporting Super's (1990) explanation that SES influences career decision-making and attainment by opening or closing opportunities, and shaping occupational concept. The sample correlation matrices of the seven observed variables is given in Table 1 for work-bound youth, while descriptive statistics represented by male and female groups are displayed in Table 2.
TABLE 1
Pearson correlations for observed variables in work-bound adolescents
Variable X1 X2 X3 Y1 Y2 Y3 Y4 Mean SD
Gender [X1] 1.00 1.47 .50 Socioeconomic status [X2] -.027 1.00 2.06 .99 Race [X3] -.016 .178 1.00 1.70 .46 Occupational aspirations (Grade 8) [Y1] .101 .098 -.060 1.00 35.38 11.65 Educational aspirations (Grade 8) [Y2] .151 .142 -.058 .217 1.00 43.69 16.28 Occupational aspirations (Grade 10) [Y3] .066 .283 -.066 .294 .282 1.00 4.10 1.36 Educational aspirations (Grade 10) [Y4] .095 .284 -.037 .235 .420 .481 1.00 3.84 1.39
Notes. N = 4,828 calculated listwise; gender (1=male, 2=female); SES reflects status in 8th grade and is based on a composite score of five variables (standardized scores, M =0.00, SD=1.00) originally designed by NELS researchers including family income, parents' education levels, and parent's occupations ( Owings et al., 1994 ); race (1=nonwhite, 2=white); occupational aspiration is a self-report value converted to socioeconomic index codes ( Stevens & Cho, 1985 ); educational aspiration is coded on a 6-point Likert-type scale calculated listwise.
TABLE 2
Descriptive statistics of work-bound adolescents by gender
Male adolescents a Female adolescents b M SD M SD
Socioeconomic status 2.08 1.00 2.03 .99 Race 1.71 .45 1.69 .50 Occupational aspiration (Grade 8) 34.28 10.48 36.64 10.49 Occupational aspiration (Grade 10) 41.38 15.34 46.31 14.65 Educational aspiration (Grade 8) 4.02 1.36 4.20 1.55 Educational aspiration (Grade 10) 3.72 1.38 3.98 1.56
Notes. N is calculated listwise; gender (1=male, 2=female); socioeconomic status reflects status in 8th grade and is based on a composite score of five variables (standardized scores, M =0.00, SD=1.00) originally designed by NELS researchers including family income, parents' education levels, and parent's occupations ( Owings et al., 1994 ); race (1=nonwhite, 2=white); occupational aspiration is a self-report value converted to socioeconomic index codes ( Stevens & Cho, 1985 ); educational aspiration is coded on a 6-point Likert-type scale calculated listwise.
a Male adolescents, n =2,563. b Female adolescents=2,265.
The MIMIC identification rule requires a scale be assigned to latent variables for identification. This was done by scaling one factor loading in each latent variable to unity with its item (i.e., fixing the factor loading to 1.00). Occupational aspirations for each latent factor were scaled to 1.0 since each was the first item in the respective latent factor. In addition, we incorporated the assumption that unstandardized regressions of observed measures on constructs (so-called "factor loadings") are equal at each point in time for each indicator of aspiration. In Figure 2 this means constraining • • 2 1 = • • 4 2 (educational aspirations at Grades 8 and 10, respectively). The regression weight • • states the relationship between the unit of measurement of the observed variable and construct ( Joreskog & Sorbom, 1993 ). The equality assumption has a specific empirical interpretation: for a given aspiration true score η1 , a unit change in aspiration will produce the same amount of change in • • 2 1 and • • 4 2 . This amounts to specifying that each of the measures of aspiration is the "same" across time. We include this set of restrictions in order to emphasize that we feel successive applications of the same measure is tapping the same construct. These restrictions are not necessary for identification and are testable by the chi-square test in the case of multiple indicators. Although we restricted these loadings to be equal, the true score variances, the measurement errors-and thus, the reliabilities-can vary over time ( Wheaton, Muthen, Alwin, & Summers, 1977 ).
Results and Discussions
The chi-square test for the model was statistically significant, Χ 2 (9) = 163.968, p < .01, indicating a good fit between the model and data. However, several researchers ( Bollen, 1989 ; Bollen & Long, 1993 ; Joreskog & Sorbom, 1989 ; Marsh, Balla, & MacDonald, 1988 ) have noted that the chi-square statistic is influenced by a large sample size (for this data set N = 4,828). In fact, Joreskog and Sorbom (1996) proposed that Χ 2 be used as badness rather than a goodness-of-fit measure in the sense that a small Χ 2 value (relative to its degrees of freedom) is indicative of good fit, whereas a large Χ 2 value reflects bad fit in SEM ( Byrne, 1998 ). In light of problems associated with the Χ 2 statistic, we examined other fit indices which also provided evidence of an acceptable data fit including GFI = .991, AGFI = .971, NFI = .957, NNFI = .904, and RMSEA = .0597. 6 These indices except RMSEA range from 0.00 to 1.00, with values close to 1.00 being indicative of good fit. According to Steiger (1990) , the RMSEA (Root Mean Square Error of Approximation) has only recently been recognized as one of the most informative criteria in covariance structure modeling, and it takes into account the error of approximation in the population and asks the question, "How well would the model fit the population covariance matrix if it were available?" ( Browne & Cudeck, 1993 , pp. 137-138). This discrepancy measured by the RMSEA indicates that values less than .05 indicate good fit, values as high as .08 represent reasonable errors of approximation in the population, values from .08 to .10 indicate mediocre fit, and those greater than .10 indicate poor fit ( MacCallum, Browne, & Sugawara, 1996 ). Based on these goodness-of-fit statistics, we conclude that our hypothesized aspiration transition model for work-bound youth fits the sample date fairly well.
We examined the maximum likelihood estimation as implemented in LISREL VIII ( Joreskog & Sorbom, 1996 ) for the model (see Table 3). The aspirations of work-bound youths were much more likely to remain stable (• •.743), and educational aspiration was a more reliable measure of the youth's postsecondary status than occupational aspiration. In order to clarify the relationship between manifest variables i.e. educational and occupational aspiration in the model and their corresponding latent constructs i.e., aspiration, factor loadings were examined. While the factor loading values of educational aspiration in both Grades 8 and 10 were statistically significant and consistent throughout the two grades (.700 and .926 respectively), the same loading values of an occupational aspiration (.422 and .427 for G.8 and G.10 respectively) were less than .50. That is, the measures did not uniformly contribute to their respective latent constructs, aspiration. Measures of educational aspirations had consistently higher loadings than measures of occupational aspirations. This suggests that the measure used for educational aspiration was a more reliable indicator of the young adolescents' aspiration construct than the occupational aspiration measure. However, we can also pull out the possibility that these work-bound students are facing uncertain passages and detours in forming their occupational aspiration in transition from school to work. That is, it indicates that these students are unpredictable and volatile in forming their future occupation. Another possibility we can pull out from the value of factor loading is the measure of choice of occupations is too broad for these adolescents to choose. We used the SEI codes to form the items. While the variability of the item makes the validity of the item increase, the reliability might be reduced for the same reason. This information can also be examined from the squared multiple correlation (R 2 ), parameter values for educational aspirations (.489 and .857 for 8th and 10th grade respectively), explained substantial amounts of item variance compared to the value of occupational aspiration (.178 and .182 for 8th and 10th grade respectively). R 2 can range from 0.00 to 1.00, and serve as reliability indicators of the extent to which each adequately measures its respective underlying construct ( Bollen, 1989 ), aspiration in this study.
TABLE 3
Maximum Likelihood estimates for model
Parameter US SE SS R 2
Lamda (• •) 1 1 1.000 .422 .178 Lamda (• •) 2 1 .189 .012 .700 .489 Lamda (• •) 3 2 1.000 .427 .182 Lamda (• •) 4 2 .189 .012 .926 .857 Beta (• •) 2 1 1.019 .037 .743 Gamma (• •) 1 1 1.392 .180 .139 Gamma (• •) 1 2 2.135 .144 .424 Gamma (() 1 3 -1.691 .202 -.156
Notes . US denotes the unstandardized solution; SE denotes standard error; SS denotes the standardized solution; R 2 equals scale reliability; t values = US/SE
Table 3 also shows the model parameter value for work-bound adolescents based on unstandardized and standardized solutions from the LISREL output. According to Saris and Stronkhorst (1984) , the advantage of the unstandardized solution is that the effects of different variables can be obtained in the original measurement units. The disadvantage of unstandardized solutions is the complication they present when trying to compare the sizes of the coefficients when computing for variables which have been expressed in different measurement units. If one wants to make such comparisons, the standardized solution has certain advantages, since all variables are expressed in the same units (standard deviations), and the effects indicate the change in the effect variable, expressed in standard deviations, caused by a change of one standard deviation in the causal variable, thereby keeping all the other variables in the equation constant. On the basis of this interpretation, the coefficients for each parameter value in Table 3 may be compared.
Implications for Practice
SEM can be utilized very effectively to address numerous research problems including nonexperimental research, and thus has become a popular methodology ( Byrne, 1998 ). Fornell (1982) stated that several desirable characteristics of SEM set it apart from the older generation of multivariate procedures. First, SEM takes a confirmatory approach to the data analysis rather than an exploratory analysis, and it lends itself well to the analysis of data for inferential purposes by demanding that the pattern of intervariable relations be specified a priori. Second, SEM provides explicit estimates of either assessing or even correcting for measurement error while traditional multivariate procedures are incapable of these aspects. Finally, data analyses using SEM can incorporate both unobserved and observed variables while the analyses using the traditional multivariate methods are based on observed measurements only.
However, Breckler (1990) warned that serious problems are also associated with SEM although the method can be useful in making sense of complex interrelations in multivariate data sets. These are (a) potential violations of distributional assumptions, (b) failure to recognize the existence of equivalent models, (c) use of the same data to both derive and confirm models, (d) modification of models without cross-validation, and (e) poorly justified causal inferences. In addition to these problems, Breckler emphasized the importance of reporting the modification history since it may be difficult to know how many changes were made to an initial model. Therefore, Breckler recommended the following for detecting some deficiency in applications of structural equation modeling. First, the data should be inspected for potential violations of the multivariate normality assumption. Distributional assumptions are likely to be violated when variables are highly skewed or when extreme outliers are present. Second, authors must make every effort to identify equivalent models and to discuss whether such models offer plausible representations of the data ( see MacCallum, Wegener, Uchino, & Fabrigar, 1993 for issues on equivalent model). Third, cross-validation should be conducted whenever an initial model is modified on the basis of the data (see Cudeck & Browne, 1983 ). Fourth, published accounts of covariance structure modeling should provide enough details of the analysis to permit replication by other investigators since unless all of a model's free parameters are clearly defined, the reader has no idea of knowing the precise model being fit. And last, whenever feasible, the data i.e., correlations or covariances should be provided as part of the published report so that other investigators may replicate the analysis and fit rival models to the data.
In this article, we promoted the use of structural equation modeling (SEM) in career and technical education research. Perhaps the most important outcome of this study was the knowledge that occupational aspirations established by Grade 8 were relatively stable for the young adolescents. Examination of the potential for systemic bias to influence the aspirations of young adolescents, particularly those of a lower social class, might be another way for educators and counselors to address the impact of SES and gender on lowered occupational aspirations. While classroom-based interventions cannot eliminate the negative effects of low SES, professionals might seriously consider their expectations, biases, and preconceived ideas about the employment potential of individuals from lower social class backgrounds and examine how these perceptions might affect the delivery of intervention programs to these individuals ( Rojewski & Yang, 1997 ). Further, it is necessary to understand the potential of early and sustained school-based career interventions for enhancing career development. Paying attention to the potential of SEM in career and technical education research, and the extent to which educational pathways in the labor market provide career guidance may help us to understand the paradigm of school to work transition, since the SEM techniques allow for the specification and testing of complex "path" models that incorporate sophisticated understanding ( Kelloway, 1998 ).
Summary
In this article we have attempted to make researchers in career and technical education aware of the usefulness of SEM by elaborating work-based issues and problems. There is no doubt that the structural equation modeling might be a great analytic tool in the career and technical education area with a variety of useful applications when used in suitable contexts, and with appropriate cautions. However we need to keep in mind Joreskog's (1993) argument that testing structural equation modeling should be regarded as a way of testing a specified theory about relationships between theoretical constructs. Browne and Cudeck (1993) , also, advised that the assessment of fit in SEM be made with careful subjective judgement based on what is already known about the substantive area and the quality of the data. What we mean by this is that researchers need to have solid theoretical background and knowledge when they attempt to apply the SEM technique to their research. Therefore, we argue again, as in all statistical analysis, that knowing the data and the sample both empirically and conceptually might be the best way to detect problems in analyzing given data.
References
Bollen, K. A. (1989) . Structural equations with latent variables . New York: John Wiley & Sons.
Bollen, K. A., & Long, J. S. (1993) . Introduction. In K. A. Bollen & J. S. Long (Eds.), Testing structural equation models . Beverly Hills, CA: Sage.
Breckler, S. J. (1990) . Applications of covariance structure modeling in psychology: Cause for concern? Psychological Bulletin , 107, 260-273.
Browne, M. W., & Cudeck, R. (1993) . Alternative ways of assessing model fit. In K. Bollen & S. Long (Eds.), Testing structural equation models (pp. 136-162). Newbury Park, NJ: Sage.
Buczynski, P. L. (1994) . Using hierarchical modeling and practical measures of fit to evaluate structural equation models. Measurement and Evaluation in Counseling and Development , 26, 328-339.
Byrne, B. M. (1998) . Structural equation modeling with lisrel, prelis, and simplis . Mahwah, NJ: Erlbaum.
Cudeck, R., & Browne, M. W. (1983) . Cross-validation of covariance structures. Multivariate Behavioral Research , 18, 147-167.
Davey, F. H., & Stoppard, J. M. (1993) . Some factors affecting the occupational expectations of female adolescents. Journal of Vocational Behavior , 43, 235-250.
Fassinger, R. E. (1987) . Use of structural equation modeling in counseling psychology research. Jounal of Counseling Psychology , 34, 425-436.
Fornell, C. (1982) . A second generation of multivariate analysis (Vol. 1). New York: Praeger.
Haller, E. J., & Virkler, S. J. (1993) . Another look at rural-nonrural differences in students' educational aspirations. Journal of Research in Rural Education , 9, 170-178.
Holland, J. L., Gottfredson, G. D., & Baker, H. G. (1990) . Validity of vocational aspirations and interest inventories: Extended, replicated, and reinterpreted. Journal of Counseling Psychology , 37, 337-342.
Hotchkiss, L., & Borow, H. (1996) . Sociological perspectives on work and career development. In D. Brown, L. Brooks, & Associates (Eds.), Career choice and development: Applying contemporary theories to practice (3rd ed., pp. 281-334). San Francisco: Jossey-Bass.
Hoyle, R. H., & Smith, G. T. (1994) . Formulating clinical research hypotheses as structural equation models: A conceptual overview. Journal of Consulting and Clinical Psychology , 62, 429-440.
Joreskog, K. G. (1973) . A general method for estimating a linear structural equation system. In A. S. Goldberger & O. D. Duncan (Eds.), Structural equation models in the social sciences (pp. 85-112). New York: Academic Press.
Joreskog, K. G. (1993) . Testing structural equation models. In K. A. Bollen & J. S. Logn (Eds.), Testing structural equation models (pp. 294-316). Newbury Park, CA: Sage.
Joreskog, K. G., & Goldberger, A. S. (1975) . Estimation of a model with multiple indicators and multiple causes of a single latent variable. Journal of the American Statistical Association , 70, 631-639.
Joreskog, K. G., & Sorbom, D. (1989) . LISREL 7: A guide to program and applications (2nd ed.). Chicago: SPSS.
Joreskog, K. G., & Sorbom, D. (1993) . LISREL 8: Users' reference guide . Chicago: Scientific Software International.
Joreskog, K. G., & Sorbom, D. (1996) . LISREL 8: User's reference guide . Chicago: Scientific Software International.
Keith, T. Z. (1993) . Latent variable structural equation models: LISREL in special education research. Remedial and Special Education , 14(6), 36-46.
Kelloway, E. K. (1998) . Using LISREL for structural equation modeling . Thousand Oaks, CA: Sage.
Kunnan, A. J. (1998) . An introduction to structural equation modeling for language assessment research [Electronic version]. Language Testing , 15, 295-332.
Lapan, R. T., & Jingeleski, J. (1992) . Circumscribing vocational aspirations in junior high school. Journal of Counseling Psychology , 39, 81-90.
Lent, R. W., Brown, S. D., & Hackett, G. (1996) . Career development from a social cognitive perspective. In D. Brown, L. Brooks, & Associates (Eds.), Career choice and development: Applying contemporary theories to practice (3rd ed., pp. 423-475). San Francisco: Jossey-Bass.
Leung, S. A. (1993) . Circumscription and compromise: A replication study with Asian Americans. Journal of Counseling Psychology , 40, 188-193.
Leung, S. A., & Plake, B. S. (1990) . A choice dilemma approach for examining the relative importance of sex type and prestige preferences in the process of career choice compromise. Journal of Counseling Psychology , 37, 399-406.
MacCallum, R. C., Browne, M. W., & Sugawara, H. M. (1996) . Power analysis and determination of sample size for covariance structure modeling. Psychological Methods , 1, 130-149.
MacCallum, R. C., Wegener, D. T., Uchino, B. N., & Fabrigar, L. (1993) . The use of causal indicators in covariance structure models: Some practical issues. Psychological Bulletin , 114, 185-199.
Marsh, H. W., Balla, J. R., & MacDonald, R. P. (1988) . Goodness-of-fit indexes in confirmatory factor analysis: The effect of sample size. Psychological Bulletin, 88 , 245-258.
Moore, A. D. (1995) . Structural equation modeling in special education research. Remedial and Special Education, 16 , 178-183.
National Education Longitudinal Study: 1988-94 (NELS:88) [CD-ROM database]. (1996). Washington, DC: U.S. Department of Education, National Center for Educational Statistics, Office of Educational Research and Improvement [Producer and Distributor].
Nichols, R. C. (1992) . The national longitudinal studies: A window on the school-employment transition. In J. A. J. Paulter (Ed.), High school to employment transition: Contemporary issues (pp. 49-60). Ann Arbor, MI: Prakken.
Osipow, S. H., & Fitzgerald, L. F. (1996) . Theories of career development (4th ed.). Boston, MA: Allyn and Bacon.
Owings, J., McMillan, M., Ahmed, S., West, J., Quinn, P., Hausken, E., Lee, R., Ingels, S. J., Scott, L. A., Rock, D., & Pollack, J. (1994) . A guide to using NELS:88 data . Washington, DC: U.S. Department of Education, National Center for Educational Statistics.
Pedhazur, E. R. (1997) . Multiple regression in behavioral research (3rd ed.). Orlando, FL: Harcourt Brace.
Quintana, S. M., & Maxwell, S. E. (1999) . Implications of recent developments in structural equation modeling for counseling psychology [Electronic version]. Counseling Psychologist, 27, 486-527.
Rojewski, J. W. (1996) . Using structural equation modeling and path analysis for advancing conceptual and theoretical positions: A technical reaction to Way and Rossman. Journal of Vocational Education Research , 21(2), 53-65.
Rojewski, J. W. (1997a) . Characteristics of students who express stable or undecided occupational expectations during early adolescence. Journal of Career Assessment , 5, 1-20.
Rojewski, J. W. (1997b) . The recent and extended past of the JVER--Understanding directions and establishing the content for dialogue. Journal of Vocational Education Research , 22, 211-218.
Rojewski, J. W. (1999) . Five things > statistics in quantitative educational research. Journal of Vocational Education Research , 24, 63-74.
Rojewski, J. W., & Yang, B. (1997) . Longitudinal analysis of select influences on the development of occupational aspirations. Journal of Vocational Behavior , 51, 375-410.
Saris, W. E., & Stronkhorst, L. H. (1984) . Causal modeling in nonexperimental research: An introduction to the LISREL approach . Amsterdam, The Netherlands: Sociometric Research Foundation.
Spearman, C. (1904) . General intelligence, objectively determined and measured. American Journal of Psychology , 15, 201-293.
Steiger, J. H. (1990) . Structural model evaluation and modification: An interval estimation approach. Multivariate Behavioral Research , 25, 173-180.
Stevens, G., & Cho, J. H. (1985) . Socioeconomic indexes and the new 1980 census occupational classification scheme. Social Science Research , 14, 142-168.
Super, D. E. (1990) . A life-span, life-space approach to career development. In D. Brown & L. Brooks & Associates (Eds.), Career choice and development: Applying contemporary theories to practice (2nd ed., pp. 197-261). San Fransisco: Jossey-Bass.
Super, D. E., Savickas, M. L., & Super, C. M. (1996) . The life-span, life-space approach to careers. In D. Brown, L. Brooks, & Associates (Eds.), Career choice and development: Applying contemporary theories to practice (3rd ed., pp. 121-178). San Francisco: Jossey-Bass.
Wheaton, B., Muthen, B. O., Alwin, D., & Summers, G. (1977) . Assessing reliability and stability in panel models. In D. R. Heise (Ed.), Sociological methodology (pp. 84-136). San Francisco: Jossey-Bass.
Endnotes
1 . The NELS:88 database is administered by the National Center for Educational Statistics, U.S. Department of Education, and represents a national probability sample of over 24,000 adolescents who have been followed at 2-year intervals since 1988 (the third follow-up occurred in 1994 when participants had been out of high school for two years). Data about selected schools and students has been collected from school administrators, parents, teachers, and students at each collection interval ( Nichols, 1992 ; Owings et al., 1994 ). Since school selection was based on unequal sampling probabilities, all frequencies and statistical analyses reflect the influence of normalized sampling weights to obtain unbiased population estimates. For illustration, our sampling pool consisted of all high school sophomores who provided valid responses to Grade 8 and Grade 10 questionnaires. Adolescents were selected if responses to questionnaires administered two years after high school graduation indicated that they had gone directly to work after graduation. This design criteria resulted in a total of 4,828 high school sophomores (2,563 boys; 2,265 girls).
2 . Bollen (1989) identified three components present in general structural equation models: (1) path analysis, (2) the conceptual synthesis of latent variables and measurement models, and (3) general estimation procedures. Path analysis was developed as a method for studying direct and indirect effects of variables hypothesized as causes of variables treated as effects. The conceptual synthesis of latent variable and measurement models is essential to contemporary structural equation techniques. The factor analysis designed by Spearman (1904) , what we now call the measurement model, emphasized the relation of latent factors to observed variables. The primary focus of the estimation process, the last characteristic of SEM, is to yield parameter values such that the discrepancy between the sample covariance matrix and the population covariance matrix implied by the model is minimal. Joreskog (1973) proposed a maximum likelihood (ML) estimator for general structural equation models that is the most widely used estimator. The use of ML estimation assumes that the following conditions have been met: (a) the sample is very large (asymptotic), (b) the scale of the observed variables is continuous, (c) the distribution of the observed variables is multivariate normal, and (d) the hypothesized model is valid ( Byrne, 1998 ).
3 . The fundamental assumption in SEM is that the error term in each relationship is uncorrelated with all the independent constructs. Studies should be planned and variables should be chosen so that this is the case. Failure to do so will lead to biased and inconsistent estimates of the structural coefficients in the linear equations and will invalidate the testing of the theory. This is one of the most difficult specification errors to test. The relationships in the measurement model also contain stochastic error terms that are usually interpreted to be the sum of specific factors and random measurement errors in the observable indicators. In cross-sectional studies, the error terms should be uncorrelated from one indicator to another. This is part of the definition of being indicators of a construct. If the error terms for two or more indicators correlate, this means that these indicators measure something else or something in addition to the construct they are supposed to measure. If this is the case, the meaning of the construct and its dimensions may be different from what is intended. It is a widespread misuse of structural equation modeling to include correlated error terms in the model for the sole purpose of obtaining a better fit to the data. Every correlation between error terms must be justified and interpreted substantively ( Joreskog, 1993 ).
4 . Latent variables are hypothetical or unobserved variables that are assumed to operate through some combination of known measures.
5 . For illustration we have chosen measured variables with single item responses. That is, the Χ was used as a pseudo-exogenous variable in this MIMIC model. We assumed the Χs are perfect measures of ξ. However, the value of the reliability might be assumed a typical value i.e., .85 if the measure is considered a fallible one. Then the error variance for SES is held fixed at (1-.85) x .variance (see Joreskog & Sorbom, p. 196, 1996 for more information).
6 . GFI denotes goodness-of-fit index; AGFI denotes adjusted goodness-of-fit index; NFI denotes normed fit index; and NNFI denotes non-normed fit index.
HEEJA KIM is Assistant Professor in the College of Education, Touro University International, 5665 Plaza Drive, Cypress, CA 90630. e-mail: heejakim@hotmail.com
JAY W. ROJEWSKI is Professor in the Department of Occupational Studies, University of Georgia, 210 River�fs Crossing, Athens, GA 30602. e-mail: rojewski@uga.edu